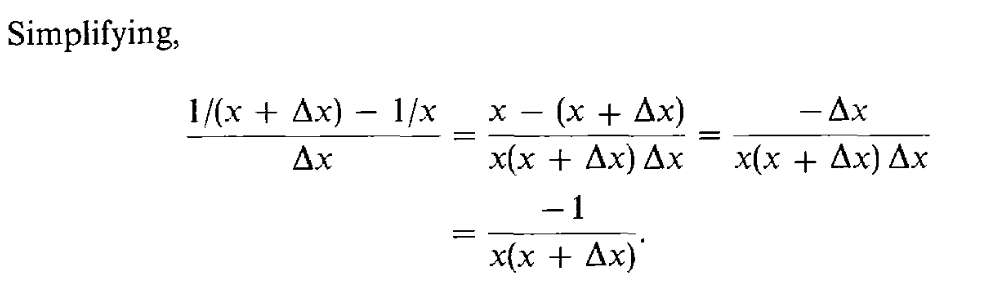So I decided to try making a web application with go and the lua template. After all, that was the original reason why I made moon-temple: so I could have an alternative templating engine text/template that comes with golang.
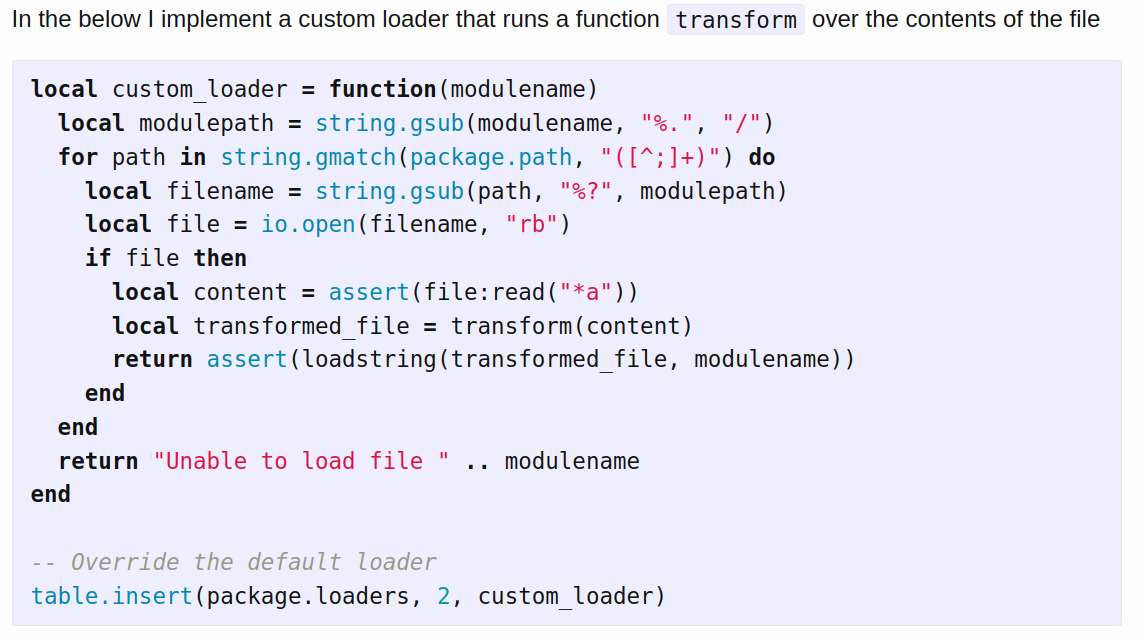
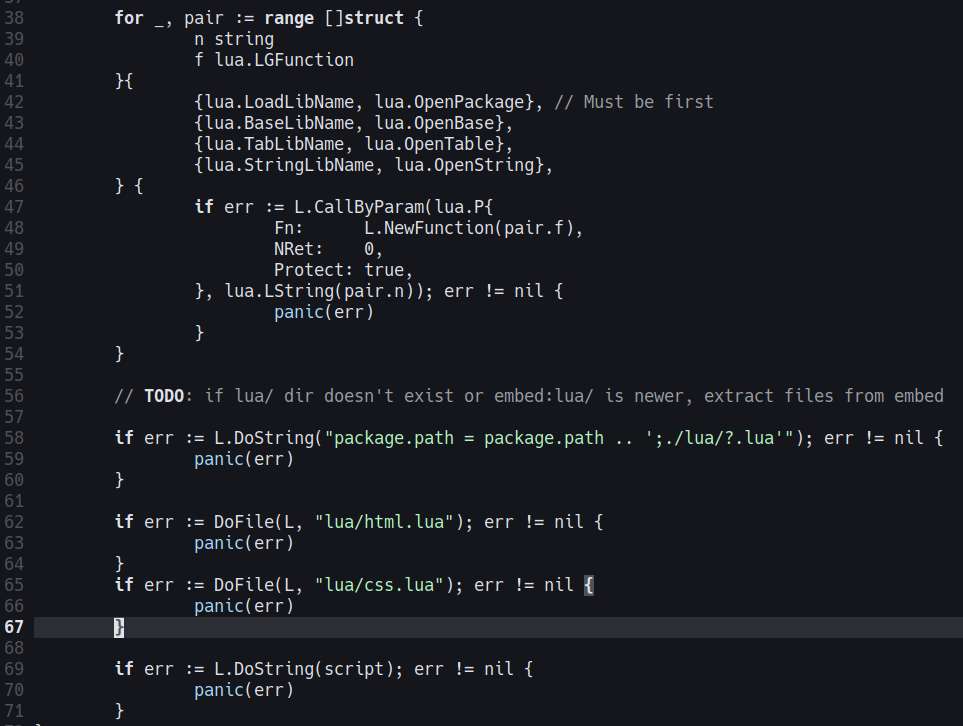
I've done some playing around with gopher-lua, and I managed to run html.lua. There's one problem though: I want the binaries self-contained as usual, so I needed to use embed.FS. Naturally, gopher-lua doesn't know how to load files from my embedded filesystem, and skimming through the docs, it appears there's no built-in support for doing that.
The first workaround I tried is to just extract the embedded files into the current directory if they are newer or doesn't exist. But strangely, running Stat() on the embedded files always return a 0 timestamp.
The second workaround I'm considering is writing a custom package.loader for lua. I found an example that I could use. Crazy enough, that example shows how I could even extend lua's syntax!? Imagine I could even go further with my DSL madness AHAHA. Or not, the editor LSP would start cussing at me if I did that. Pretty neat stuffs though.
Right now, I'm wondering if I should do some maintenance work on moon temple. Tasks like refactoring, cleaning up, add do some proper releases, that kind of stuffs.
Or I could start a new project. I want to try html.lua with a golang backend, and webui as the frontend. Then try htmz for general frontend/backend interaction.
Or not, I should invest more time creating stuffs with godot and blender.
This early afternoon, I gave the six younger puppies, and the 2 adult puppies, a bath. Not much else to say about it, except that it's quite tiring to do, so I really should avoid doing it all at once.
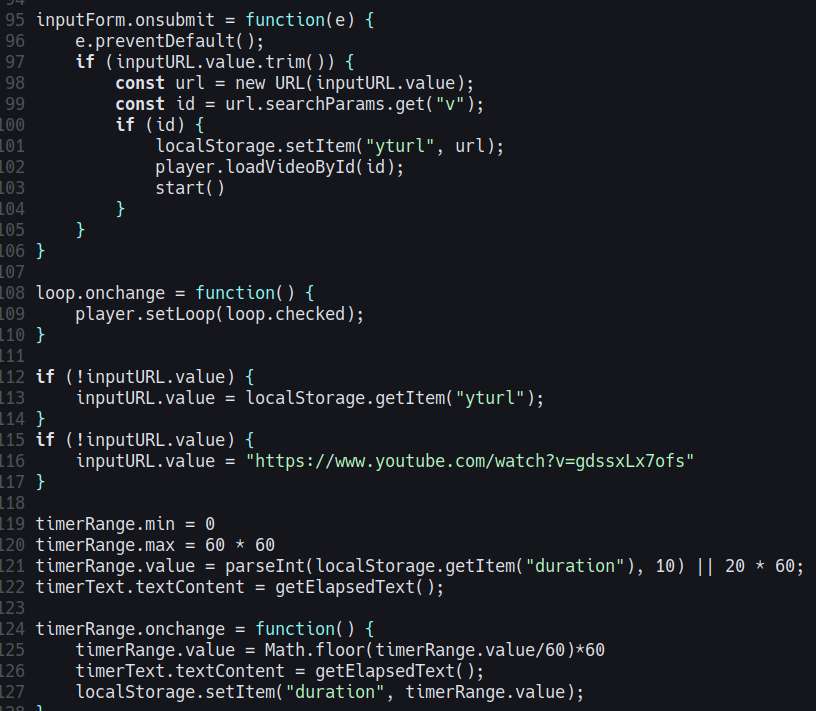
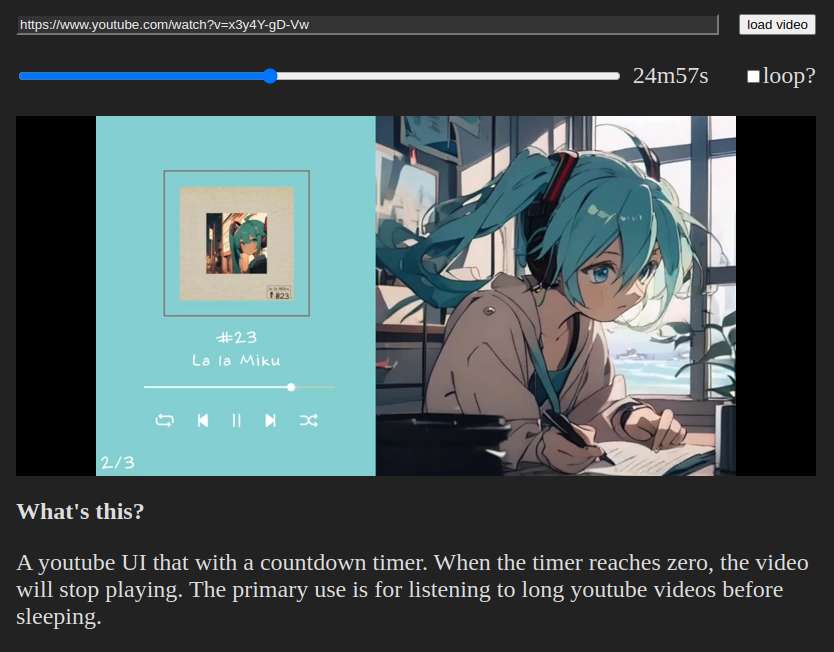
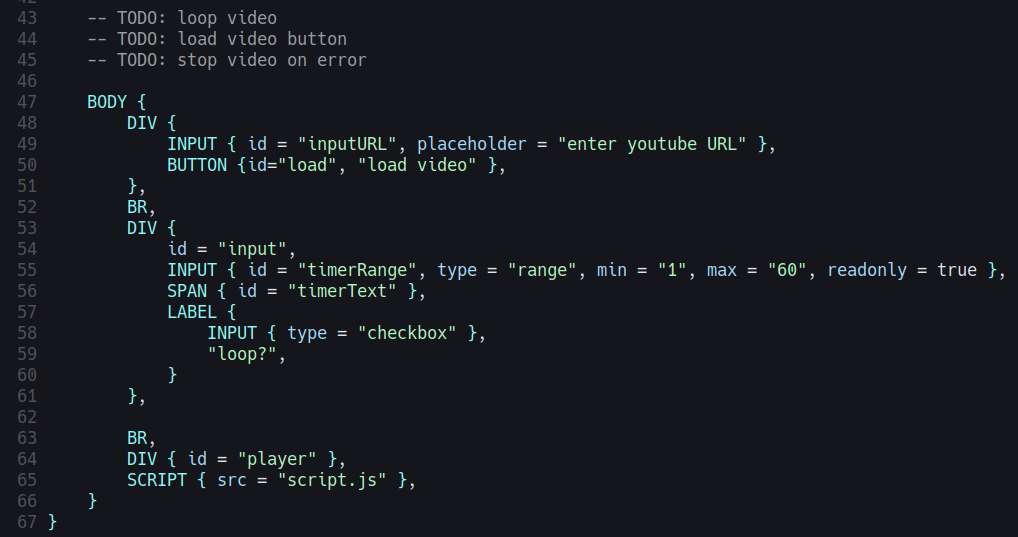
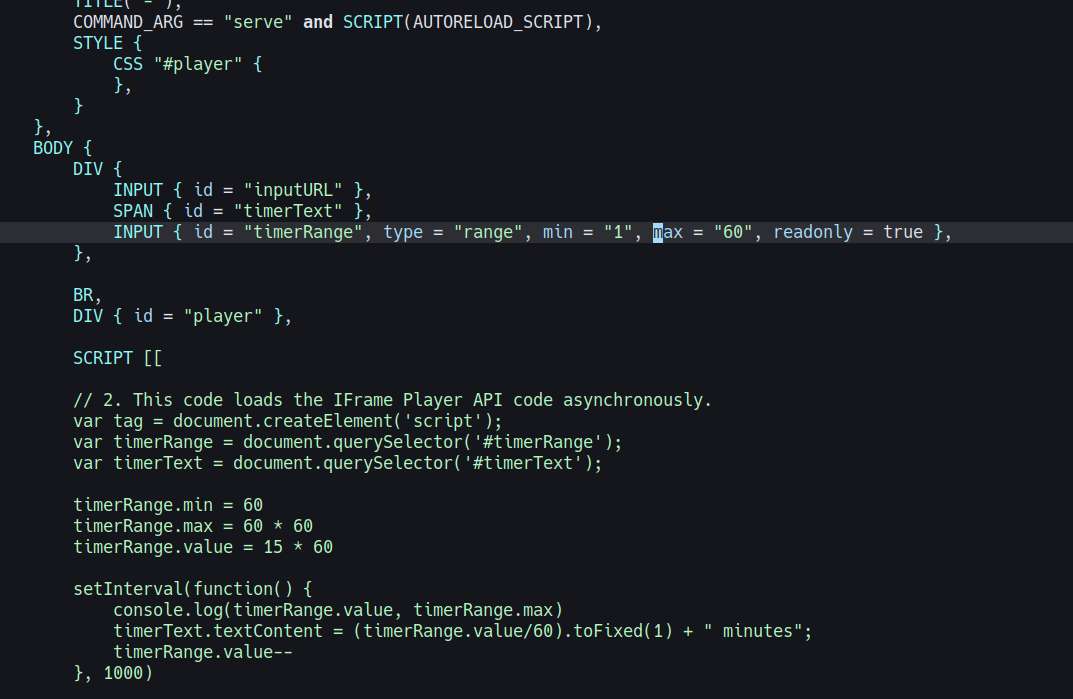
There, I finished my shitty youtube UI. Basically, it's just a youtube player but with a countdown timer. The purpose of this is so I could listen to longer youtube videos without draining my phone battery.
I always listen to youtube before going to sleep, it really helps me fall asleep faster, it keeps me from thinking a bunch of things that keep me awake.
I continued reading "calculus: an infinitesimal approach". I'm still following so far, but I don't quite get the increment theorem. For starters, why would ∆y be infinitesimal? If the book is referring to ∆y in the equation
∆y = f(x+∆x) - f(x)Of course, it's actually referring to a different(?) ∆y, the book is saying the ∆y in the equation
∆y = f'(x)∆x + ε∆xWhat I've learned just now:
- tagential line defined as l(x) - b = f'(a)(x - a) which is a line that intersects the point(a,b) with slope f'(a)
- change in y along the curve = f(x + ∆x) - f(x) change in y along the tangent line = f'(a)∆x
- differential of y and differential of x
- the change in y along the tangent line is called the differential of y, and is notated as dy, as opposed to ∆y, which is the changed in y along the curve
- dx and ∆x is the same, but dx is also used for notation consistency it seems
(x + y)~ = x~y~(x~ + y~)~
x + y = xy(x~ + y~)
x00~
(x^2)~ = x~2
x~^2 = x~2
x^(y~)
sqrt(x) = x^0.5 = x^2~
cbrt(x) = x^0.333.. = x^3~
(x^a)x~ = (x^a)(x^-1) = x^(a-1)
(x^a)^b = x^(ab)
(x^a)(x^b) = x^(a+b)
x^(n^-1)
x^(n^m) =? (x^n)^m
x^(2^3) =? (x^2)^3
x^8 =? (xx)^3
x^8 =? xx xx xxOh well, for today's morning, I've thought about why 0~ is undefined. Wikipedia gives me a lot of answers, but for some reason it still doesn't sit right with me. I should continue on with the calculus book, anyway, until I find another equation that seems difficult to solve with exponential notation.
I'll probably want to explore logarithms as well later.
= [(x+y)~ + -x~]y~
= [(x+y)~-x~(x+y + -x)]y~
= (x+y)~-x~yy~
= -(x+y)~x~Here's the list of theorems that I may find useful in my tedious journey of purely using exponential notations:
xy = (x~y~)~
x + y = x(1 + x~y) = y(1 + xy~)
x + y = xy(x~ + y~)
(x + y)~ = x~y~(x~ + y~)~
a(x+y)~ = [a~x+a~y]~I will set aside that thought, and I will continue forth. Uhh, why am I writing like this? I have a bloody headache right now, mostly because of I ran out of coffee, and caffeine withdrawal gives me a really bad headache.
Continuing from last friday, I found about multiplicative inverses conforming to de morgan's law:
xy~ = (x~y)~
x~y = (xy~)~
xy = (x~y~)~
[1/(x+y) - 1/x]/y
= [(x+y)~ - x~]y~
= (x+y)~y~ - x~y~
= [(x+y)y]~ - x~y~
= [xy+yy]~ - x~y~ // how do I go from this...
= ...
= -(x+y)~x~ // to this
(x+y)~ = ~x + ~y
(x+y)~ + -x~
= -y(x+y)~x~
= -(x+y)~x~y
(x+y)~ + x~
= (x+y)~yx~
-------------------------
= (x+y)~ + -x~
= (x+y)~xx~ + -x~(x+y)(x+y)~
= (x+y)~xx~ + -x~(x+y)(x+y)~
= [ xx~ + -x~(x+y) ](x+y)~
= [ x + -(x+y) ](x+y)~x~
= [ x + -x -y) ](x+y)~x~
= -y(x+y)~x~
x + y
= xyy~ + yxx~
= xy(y~ + x~)
x~ + y~
= x~yy~ + y~xx~
= x~(yy~ + y~x)
= x~y~(y + x)
x~ + y
= x~yy~ + yxx~
= yx~(y~ + x)
x + y~
= xyy~ + y~xx~
= y~x(y + x)
x~ + 0~
= x~0~(0 + x)
(x+y)~
= xy(x~ + y~)~
= [x~y~(x~ + y~)]~
= [(x~x~y~ + x~y~y~)]~
= [(x~2y~ + x~y~2)]~
= [(x~2 + x~2)y~]~
= (x~2 + x~2)~y
= (2x~2)~yLet me try again:
(x+y)
= xy(x~ + y~)
(x+y)~
= x~y~(x~ + y~)~
(x+y)~
= x~y~(x~ + y~)~
(x+y)~
= [ xy(x~ + y~) ]~
= [ xyx~ + xyy~ ]~
(x+y)~
= [xy(x~ + y~)]~
= xy(x~ + y~)]
1/(x+y) - 1/x
= (x+y)~ + -x~ // (A)
= (x+y)~xx~ + -x~(x+y)(x+y)~
= (x+y)~xx~ + -x~(x+y)(x+y)~ // common: x~,(x+y)~
= [ xx~ + -x~(x+y) ](x+y)~
= [ x + -(x+y) ](x+y)~x~
= [ x + -x -y) ](x+y)~x~
= -y(x+y)~x~
= -(x+y)~x~y // (B)Welp, this sucks, I feel like I'm going in circles. I should write and separate the equations that are shown to be true first.
I just finished breakfast, which is quite late for a reason. Around hour ago, my husky dog went through a hole in the wall, and was set free in the swampy wilderness. I didn't realize though until I saw two people in the swap yelling to me about our dog attacking their ducklings. I said, that can't be, all of our dogs are in the house. Then I went around and noticed I don't see the big ole furry dog anywhere. Oh fuck, I thought.
I didn't really have any choice though, but to go out and search for my dog. I screencaped a google map and annotated it to make it easier to explain.
- In the image, the husky dog went through a hole on (B) I really don't want to wade through the swamp if possible, so I went through the front gate first (F) - I walked around neighbourhood street first (1) and (2) and didn't see any husky dog - I checked out the aggrived duckling owners, went through their lot (3) and walked through the swampy terrain. I didn't see or hear anything. - At this point, I went back inside and put some long pants and boots, because the swamp likely consists of various nasty household gooey waste, not to mention the possible snakes. - It's hard to see anything because of the really, realy tall grasses, so went to the discontinued road for a better view of the surroundings (4) - Walking through the abandoned road wasn't any easier, but at least it was dry. It had a lot of sharp tall grasses (wild sugarcane I think they are called), so I only tried walking on the edges. (5) - My mother was on a tricycle yelling, searching for me and the dog (C) - While I was on the way to (6), I heard a splash in the swamp, followed by chickens flying. From point (C) looking at point (A), I finally found the the husky dog - I slowly trudged back to point (A), hoping the husky dog didn't run off to somewhere. Thankfully, the husky was still there standing, waiting for chickens to munch on. I put him on a leash, and made our way back to the dry lands. (7) - I saw a dead orange tabby cat (A), which suspiciously looked like our cat, but I'm not sure. I didn't check further though, because the husky might actually try eating it.
And there, it was quite a terrible morning to start a day with, but I'm just glad I found the husky safe. Worse case scenario, my dog went further out, in the neighbouring streets, never to be found again. I admit, I did kind of enjoy walking in the swamps, just the like old days.
Around 18:30, there's was a traffic incident just across the street from my house. A tricycle and a motorcyle crashed into each other. Me and my mother curiously watched from the front gate. It appears no one was seriously injured. There was an ambulance, but I didn't see any stretchers, or anyone gravely injured that needed immediate medical attention. It was for the most part, a nothingburger, for anyone not directly involved in the incident. Maybe. It's hard to see anything from where I stood.
In my whole life, I strangely don't think I've ever seen a serious traffic accident in person, and I say this as someone who used to walk home alongside the highways a lot back in the old days. Or maybe there was, and I just can't remember.
I'm wondering now, why do I need to add the two fractions together before I could simplify it. Isn't there another way? That does sounds like a math trick that I must do without knowing why. That's what I tried before, but I couldn't get any further:
[1/(x+y) - 1/x]/y
= [(x+y)~ - x~]y~
= (x+y)~y~ - x~y~
= [(x+y)y]~ - x~y~
= [xy+yy]~ - x~y~ // how do I go from this...
...
= -(x+y)~x~ // to this
x~ + y~ = (x+y)x~y~
x~ + y~ = [(x+y)~x]~y~
x~ + y~ = [(x+y)~x]~y~ // TODO:
xy~ = (x~y)~ // ooh, this is actually true
x~y = (xy~)~ // woah, this holds as well
xy = (x~y~)~ // this too!?!?
xyz = (x~y~z~)~ // cool, it generalizes to arbitrary number of terms
// actually ~ behaves a like de morgan's law
x~ + y~
= (x + y)/(x*y)
x numerator
-----
y denominatorTo solve `1/x + 1/y`, I just need to make them have the same denominator:
1/x + 1/y
= (1/x)(y/y) + (1/y)(x/x)
= y/xy + x/xy
= (x+y)/xyNow I just need to translate this to exponential notation:
x~ + y~
= x~yy~ + y~xx~
= (yy~ + y~x)x~
= (x+y)x~y~----
Back to the previous problem, I need to simplify `(1/(x+y) - 1/x)/y`:
Simplify the numerator first
1/(x+y) - 1/x
= (x+y)~ + -x~ // (A)
= (x+y)~xx~ + -x~(x+y)(x+y)~
= (x+y)~xx~ + -x~(x+y)(x+y)~ // common: x~,(x+y)~
= [ xx~ + -x~(x+y) ](x+y)~
= [ x + -(x+y) ](x+y)~x~
= [ x + -x -y) ](x+y)~x~
= -y(x+y)~x~ // (B)
(1/(x+y) - 1/x)/y
= [ (x+y)~ + -x~ ]y~ // (A) times y~
= [ -y(x+y)~x~ ]y~ // replaced (A) with (B)
= -(x+y)~x~ // yy~ are inverses, so yy~ = 1
= -1/(x+y)*x----
I'm still not sure if avoiding fractional notation is better, but at least so far I've managed to avoid relying on special rules to do algebraic simplifications. I still don't know how the book was able to get `-1/(x+y)*x`, it just seems "magic" for me. Well actually, looking closer, the book did use the same trick by making both terms use the same denominator. It only just skipped lots of steps in between.
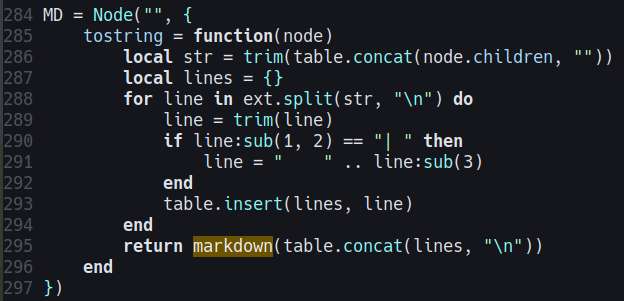
Added some markdown library, so my logs would look well formatted. The markdown library is actually using the older spec, so triple ``` isn't event supported. It's good enough for now, but ideally, I should just avoid markdown and just put longer notes on a separate lua page.
I also gave myself a haircut today. By haircut, I mean I trimmed excess hair so the hair would stop poking my eyes, and I could save some soap and shampoo. Cutting my own hair saved me about $2, and importantly saves me the anxiety of having to go outside. Needless to say, my hair looks like shit, before and after.
But as the saying goes, even stinkiest fart eventually goes away. I'm sure in the whole history of mankind someone said that, surely. I just remembered a certain shark saying "fart in the wind", which is identical in meaning.
I skimmed over the book of abstract algebra last night, I didn't find anything I could use.
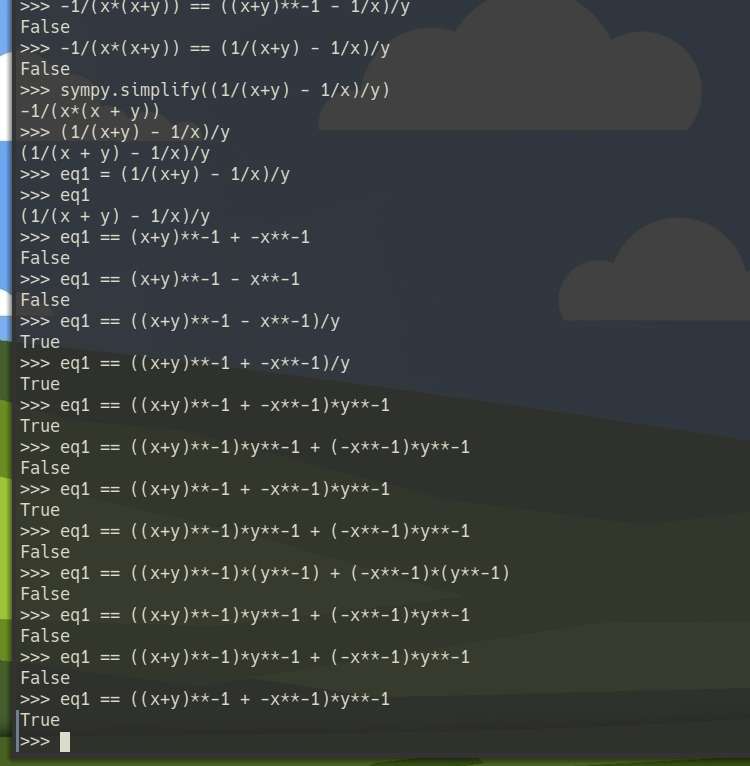
Played around more with equations, on paper, vim, and with python/sympy.
What I just realized is that, 1/(x+y) - 1/x can no longer be simplified. The book actually does simplification with (1/(x+y) - 1/x)/y
Second realization is that sympy does not automatically simplify when comparing equality between expressions. I seriously started questioning and doubting myself when it returns false with (a*b)*x == a*x + b*x.
I actually need to do simplify((a*b)*x) == simplify(a*x + b*x)
That said, the furthest simplification I got was
(1/(x+y) - 1/x)/y
= (x+y)^-1*(y^-1) + (-x^-1)*(y^-1)
(1/(x+y) - 1/x)/y
= (x+y)~y~ + -x~y~
(1/(x+y) - 1/x)/y
= (x+y)~y~ + -x~y~
= [(x+y)y]~ + (-xy)~
(1/(x+y) - 1/x)/y
= -1/(x*(x + y))
x~ + y~
= (x + y)/(x*y)
= (x + y)(x*y)~Ultimately, my goal is to show (to myself) that I can do algebraic manipulations without using fractions. It's a hill I'm willing to die on, probably. Or at least, lose a leg.
Aha, I found what I'm looking for:
(ab)^-1 = (a^-1)(b^-1)Now, I'm trying to follow an example of how to get the derivative of 1/x. Once again, whenever I see I fractions, I frequently scratch my head how did the book go from this to that. I should probably learn the basics how to combine fractions together, but I am weirdly fixed on notational purity, so I want to see could I solve this just in terms of exponents.
First, consider the equation:
1/(x+y) - 1/x
= 1/(x+y) + -1/x
= (x+y)^-1 + x^-1
(x+y)^-1 =? (x+y)1^-1
x^n = (x^a)(x^b) where n = a+bNope, it's even more complicated now, I've further strayed away from the light, the opposite of simplifying.
Oh well, I think I'll read the book of abstract algebra first.
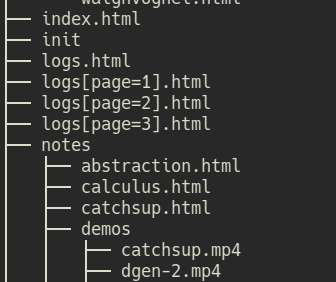
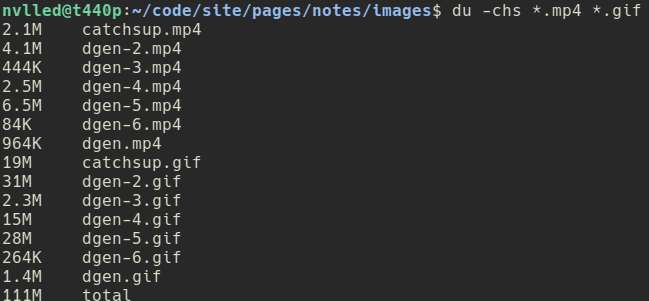
Modified the build action so that local links with filename parameters will be included in the build files. I also updated converted the .gif files to mp4, which reduced the overall size from ~100MB to 20MB. Even though I only worked for about an hour or two, I feel like I got a lot of things done. Useless stuffs to be sure, but at least I felt productive. Also, the owl has just finished singing.
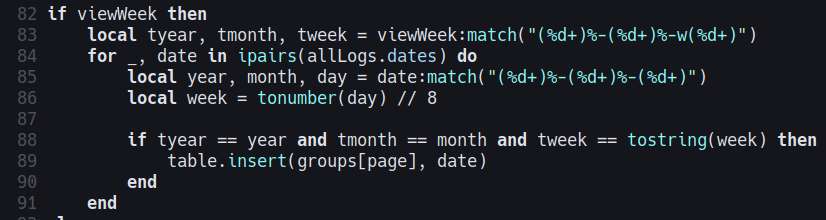
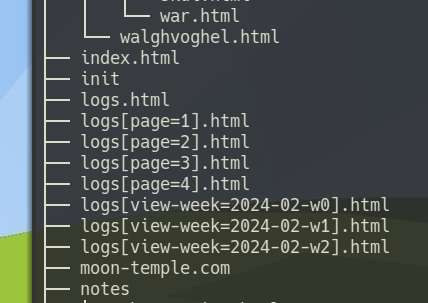
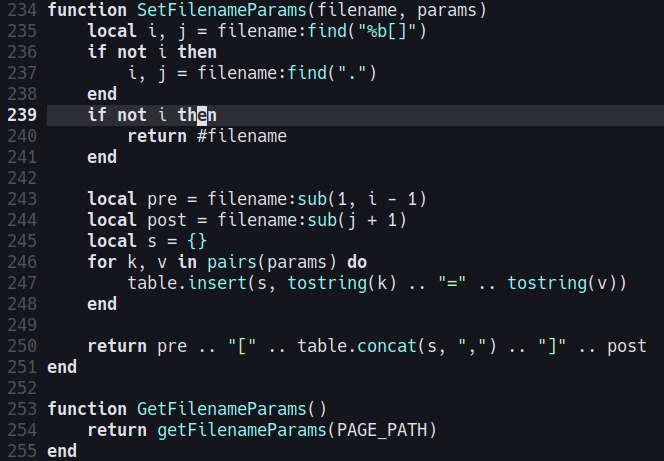
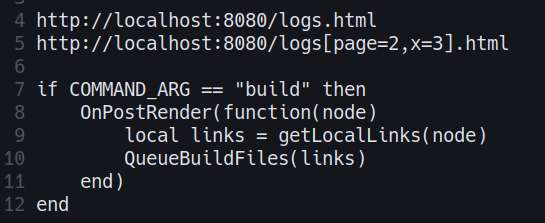
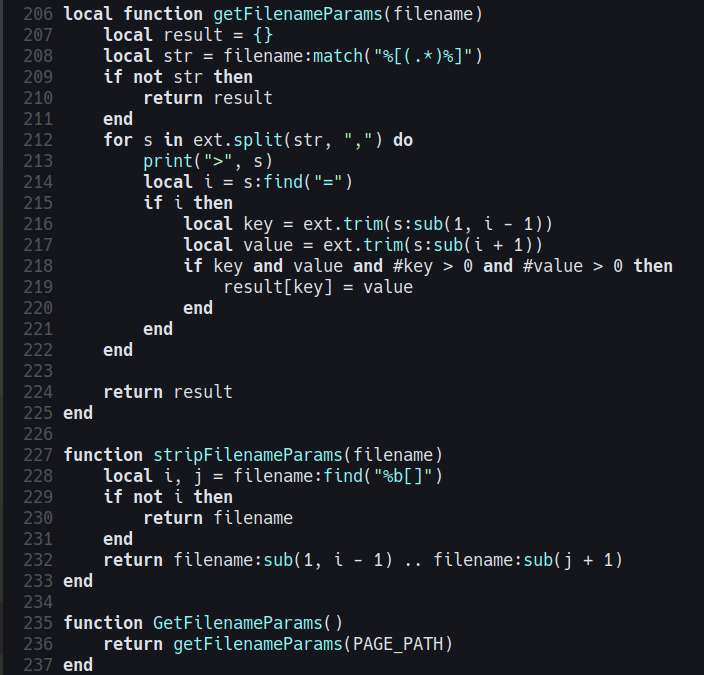
Finished the pagination. In my previous site generator, I used query parameters for the page numbers, but this time I used a custom file parameters, such as:
/page[page=1,param=2,xyz=foo].html
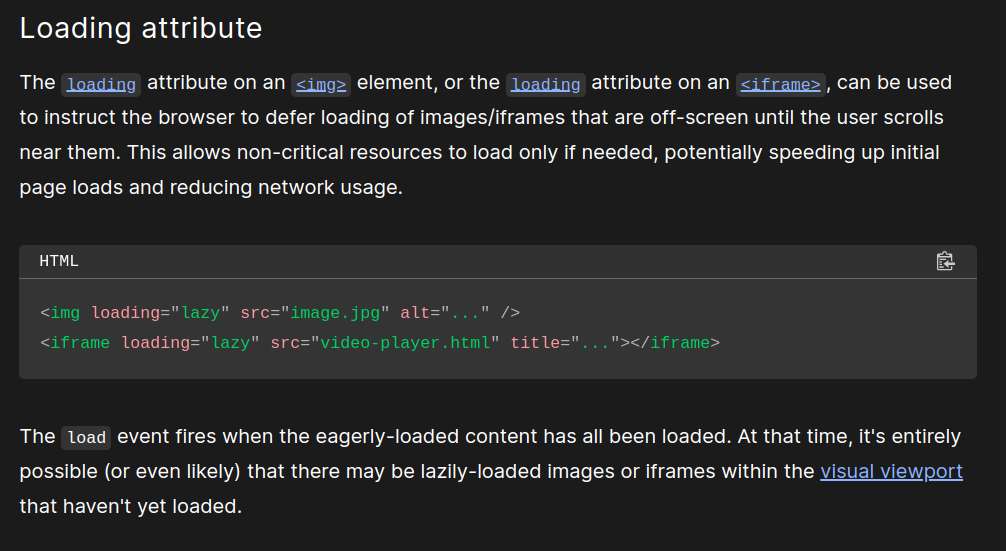
This way, the local links will be the same on dev server, and on the html build files. I also discovered that I can lazy load images by doing `<img loading="lazy" ... />.` This should at least reduce page load time and bandwidth usage. It's a nice work-around for not being able to generate thumbnails for the mean time.
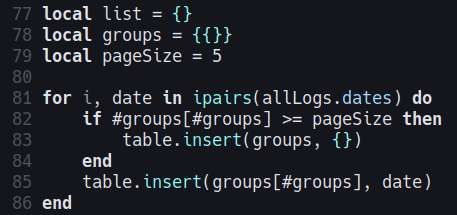
I started implementing pagination for the logs page, this is too avoid loading too many images in one page. The ideal, alternative solution would be to generate thumbnails for my screenshots, but for now I want moon-temple to be fully cross-platform without any dependencies, and for that, I can't rely on external image libraries to resize images. It's possible to write a pure lua implementation of png resizing, but that's not going to be an easy task.
Didn't do much this morning, aside from cleaning and walking around. I also spent some time answering a questionnaire for a job assessment. I got an email back this weekend from a job application that I sent months ago, either I completely forgot about or just gave up on it. I'm not expecting much, I don't have strong feelings one way or the other, rejected or not, life carries on as usual.